NMR Precision Teslameter PT2026
NMR Magnetometers
Advantages
+ Secondary standard
+ No drift
+ Total field reading
+ Extremely precise
Constraints
– Measurement of uniform, continuous, or slowly varying fields
– At low field requires a large sample
If a nucleus possesses spin, it tends to align itself with an external magnetic field. However, by precisely supplying the additional energy required, the nucleus can be induced to flip into the opposite spin state.
Nuclear Magnetic Resonance (NMR) occurs when the radiofrequency field applied to a sample has exactly the right frequency, called the Larmor frequency, to induce this spin flip.
The core of an NMR magnetometer is simply a coil wrapped around a sample. The coil provides the radiofrequency energy required to induce spin flips in the sample. The best response is obtained by placing the coil axis perpendicular to the field. Resolution is limited only by the resonance width, which, depending on the sample material, can be very narrow, on the order of 1 Hz.
Moreover, NMR always measures the total strength of the field rather than a single component. Finally, and most importantly, since the gyromagnetic ratio is a physical constant, the NMR magnetometer exhibits virtually no drift and requires no calibration.
It turns out that the energy difference between aligned and anti-aligned nuclear states depends linearly on the field intensity. Thus, the ratio of resonance frequency to field intensity is a physical constant called the gyromagnetic ratio (gamma).
It is about 42.5 MHz/T for protons (hydrogen nuclei). Other nuclei also exhibit NMR, but with a different gamma, for example, 6.5 MHz/T for deuterium and 40 MHz/T for fluorine. To extend the NMR measurement range, we can use a sample with a different gamma. A deuterium sample has a gamma that is 6.5 times lower than protons, so the same frequency range will measure fields 6.5 times higher.
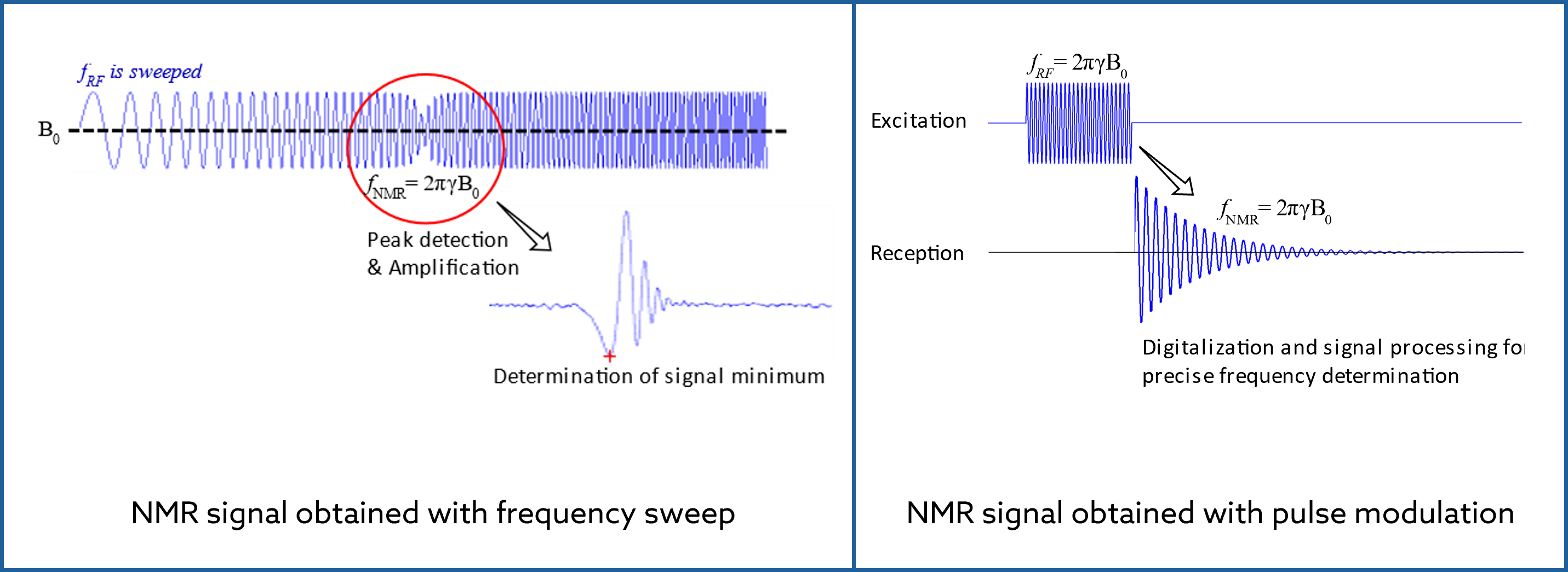
There are two fundamental methods of detecting Nuclear Magnetic Resonance. The continuous sweep approach is similar to tuning a radio: we slowly adjust the frequency until we “tune in” to resonance. To be able to detect it, we must pass through the resonance frequency several times, which means we must modulate either the frequency or the magnetic field.
The pulsed wave approach, on the other hand, is akin to ringing a bell: we strike the sample with a broad-band pulse, and the sample absorbs and re-emits at the Larmor frequency. The pulsed mode approach requires fast-switching modern electronics but is more direct and offers greater precision and information.
After resonance, the sample is usually allowed to release the absorbed energy and return to its original spin-aligned state. This limits the measurement frequency to about 10-100 Hz. Additionally, to reduce variability, many such measurements are often averaged, producing effective measurement rates approaching one second. Therefore, NMR is generally useful only for slowly changing fields.
If the field is not uniform, one side of the sample will resonate at a different frequency than the other side. The resonance peak broadens and flattens until it disappears completely into noise. This phenomenon determines the field homogeneity limit in NMR.
There are also practical limitations to the useful range of NMR. For low magnetic fields, nuclei are only weakly aligned, and the NMR response fades. The simplest solution is to use a larger sample, thereby increasing the number of participating spins; however, at some point, the sample size becomes impractically large for a versatile probe.
The NMR response is excellent for high magnetic fields, but the instrument’s RF generator and the coil’s inductance impose an upper limit on attainable frequencies. The coil’s size and number of turns are reduced to decrease inductance. A practical limit is reached when the coil is reduced to a single small loop.

The coil around the sample is an inductance, with a response that decreases at high frequency. If we add a parallel capacitance, we create an LC resonator, which, if tuned to match the Larmor frequency, significantly improves the sensitivity of NMR signal detection. For this reason, NMR probes require tuning.